DEPM Estimation

Jonathan Smart

2020-02-10

Source: vignettes/DEPM_Estimation.Rmd

Load the DEPM and tidyverse libraries.

library(DEPM)
library(tidyverse)

Introduction

The traditional Daily Egg Production Method (DEPM) has been used to determine spawning stock biomass of fish populations for over 40 years. While this package is primarily designed to facilitate the use of revised approaches to DEPM, including (stage-based estimation of daily egg production (McGarvey et al. 2018) and female adult size-dependence of population numbers and batch fecundity (DEPMWt; McGarvey et al in review), many aspects of the approach (i.e. estimation of some key DEPM parameters) remain the same. Therefore, the traditional DEPM methods are also included in this package. Here, an example of the DEPM approach is given using South Australian snapper (Chrysophrys auratus).

Necessary data

Five datasets are required to use the DEPM approach:

  • Egg density data to estimate daily egg production (\(P_{0}\))
  • Adult sex ratios to estimate R
  • Female spawning fractions to estimate S
  • Female total weights to estimate mean adult female weight (W)
  • Female total weight and batch fecundities to estimate mean female fecundity (F)

Spawning Area (A) is not calculated as part of this package but its estimates will be included as one of the final steps.

DEPMWt parameter estimation

Daily egg production (\(P_{0}\))

Daily egg production is estimated using a stage-based estimator (McGarvey et al. 2018) via the function Estimate_P0() which requires a dataset that has been formatted as such:

This dataset is in a long format where every row is a density estimate of the eggs in each stage of each sample. This dataset contains several columns that must include:

  • Site - which represents each sample in the data (i.e. one plankton tow a location). It’s variable name must be specified as an argument using site =
  • Density - the number of eggs in a single development stage in a metre cubed of seawater. The function will automatically determine the density column based on similar names (i.e. dens, density, DENSITY or other similar names). However, there cannot be multiple density columns.
  • Age - the age in days of each egg stage in each sample. The function will automatically determine the Age column based on similar names in a similar manner to the Density variable
  • Hatching time - The age in days where the eggs in each sample are estimated to hatch (usually differs based on temperature). The function will automatically determine the Hatch column based on similar names in a similar manner to the Density variable
  • Z - a pre-specified level of egg mortality used to determine \(P_{0}\). Multiple values can be provided to simultaneously determine different values of \(P_{0}\) based on this parameter. Instruction on how to do this and how to perform sensitivity tests are provided in the final section of this vignette.

Additional columns can be included in the dataset, so the user does not need to remove variables that could be useful to them later on. For example, in the egg_data dataset, the Stage_num variable represents the development stage of each density estimate in each sample. However as each row of this dataset is a different observation, this variable is not needed by the function.

The function also has the ability to break the data down spatially and temporally. If the Region and Time arguments are not used then \(P_{0}\) will be estimated using all of the data. If you provide either Region or Time then a \(P_{0}\) will be returned for each Region/Time combination. Therefore, a time series of data can analysed in a single function call. Here is an example using 4 DEPM surveys conducted in different areas but in the same year. The results are returned as a dataframe where each row is a survey and the estimate, standard error and specified mortality are returned.

Spawning fraction (S)

Spawning fraction is estimated using the function Estimate_Spawning_fraction() which requires a dataset that has been formatted as two columns: 1) the number of females in spawning condition and 2)the total number of females. Each row represents a sample and the spawning fraction is estimated using a ratio estimator.

The correct columns in the dataset will be detected by the function. The column with the total number of females should be called “Total”, “Tot” or something similar. The column with the number of spawning females can include the term “spawn” or “yes” depending on how your dataset is setup. Ours is named “yes” as we had a “yes” or “no” designation for spawning fish.

Similar to other functions, specifying the Region or Time argument with relevant column names will group the estimates according to specific surveys. However, here an example is given without a region or time grouping. The results are returned as a dataframe with the estimate, its variance, the standard error and its CV. Each row represents a survey.

Female weight and fecundity

The key difference between teh DEPMWt approach and the traditional DEPM is how female weight and fecundity are handled. In the DEPMWt approach, female weight is broken into discrete weight bins and their variance is described using a multinomial distribution. However, in the traditional DEPM approach, the W parameter is used and represents the mean female weight and its variance. Similarly, fecundity is also expressed as the mean number of eggs per adult female and its variance.

Fecundity

Fecundity needs to be summarised in a couple of ways. Firstly, a batch-fecundity relationship is required for gonad free weight which can be used to predict the fecundity of fish whose histology has not been examined. This relationship can be estimated using the Estimate_Batch_Fecundity() function. This function is quite useful as it can return three sets of outputs:

  • A data.frame of parameters and their variances for the relationship (these can also be printed to the screen) by setting return.parameters = TRUE.
  • A dataframe with the predicted fecundity for each weight along with SE and 95% confidence intervals
  • A dataframe with the predicted fecundity at specified weights and their variance and SE.

The batch fecundity estimator uses an allometric relationship which allows for wider variance with larger weights. Therefore, there are four parameters returned, alpha, beta and two sigma parameters that determine how variance changes with weight. A dataframe with two columns must be provided that includes gonad free weight in grams and the number of eggs for that fish. The function will determine which is which based on their scales (number of eggs > Wt in grams). A set of starting parameters are required and are provided to the start_pars argument as a list. The estimated parameters are printed to the screen if verbose = TRUE.

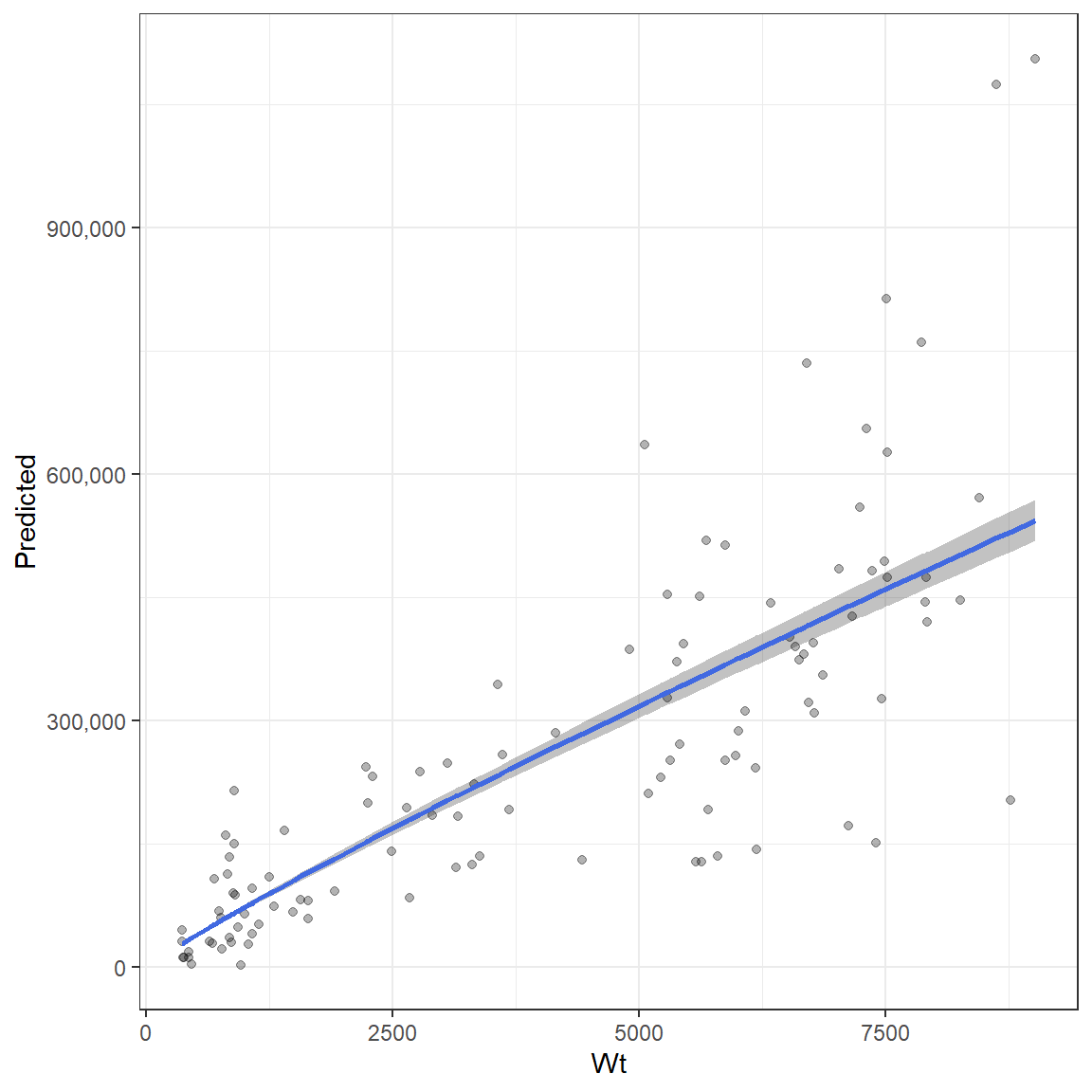
This function can also automatically estimate batch fecundity by allowing some of the parameters to be fixed. This is performed using the fixed.pars argument which requires a vector with the listed parameters to be fixed. Determining whether this is necessary is done by running the function and returning the parameters.

For South Australian Snapper, the variances of the alpha and Sigma0 parameters are clearly overestimated. The function fixes this by running the model twice; once with all four parameters estimated and then again with the fixed parameters (ones which were estimated correctly the first time) held at their estimates from the first model. For example:

Weight The parameters for W and F are determined using a single function called Estimate_mean_W_F(). This function requires:

  • A dataframe of weight.data which will be used to estimate W and estimate F based on the fecundity-at-weight relationship.
  • A character string for TotalWt indicating the variable name for Total weight in grams. This will be used to estimate W.
  • A character string for GonadFrWt indicating the variable name for gonad free weight in grams. This will be used to estimate F for each weight. If gonad free weight is not available, then this argument can be left NULL which will prompt the function to estimate fecundity based on total weight instead. NOTE: If total weight is used to determine F then total weight should be used in return batch fecundity parameters from Estimate_Batch_Fecundity() as well
  • A dataframe of batch fecundity relationship parameters from Estimate_Batch_Fecundity() with return.parameters = TRUE. The object returned from this call can be directly provided to Estimate_mean_W_F().

As with other functions, providng Time/Region variable names will group the results either spationally, temporally or both. Here a Region grouping is applied.

Spawning Area (A)

Spawning area is the only DEPM parameter that is not estimated in this package as this is typically done using GIS methods. However, the Spawning area object can be created manually by taking another parameter object (P0, S or R are good choices) and using its Time/Region groupings to create new object. As this example has one survey from 4 regions in a single year, only the Region variable needs to be carried across. A new variable can then be added with the location in the correct order in that column. Spawning Area is a precise quantity and therefore does not require a variance. Note that spawning area must be in metres squared.

Combining parameters as inputs for biomass estimation

With all of the parameters now available to calculate spawning stock biomass, these now need to be combined into a dataset that can be input into the Estimate_DEPM_Biomass() function. For the DEPM approach, two objects are needed:

Combining parameter estimates

A dataframe of all of the parameter estimates can be assembled using combine_estimates() where each of the parameter objects are provided as arguments.

Where a parameter is estimated as time invariant, it will be automatically allocated to all of the Region or Time groupings applied for the other parameters. Here this occurs for S. However, if a particular parameter is missing in one instance but is not time invariant, it will not be carried over and NA will be returned. In this situation, it will need to be inserted manually. For example, lets pretend that R is missing for “SSG”:

Combining parameter variances

Variance estimates are needed by Estimate_DEPM_Biomass() in order to determine the precision of the biomass estimates. These are provided in the same fashion as the parameter estimates using combine_variances().

The same manual insertions can be performed on this object:

Spawning Stock Biomass Estimation

All of the hard work is done once all of the parameters and their variances have been estimated and organised. The final step is to combine them using Estimate_DEPM_Biomass(). This function requires each of these objects and will return a list of results which include the spawning stock biomass and total number of females.

The list of dataframes returned from the function can then be saved and used for plotting

Plot biomass with SD

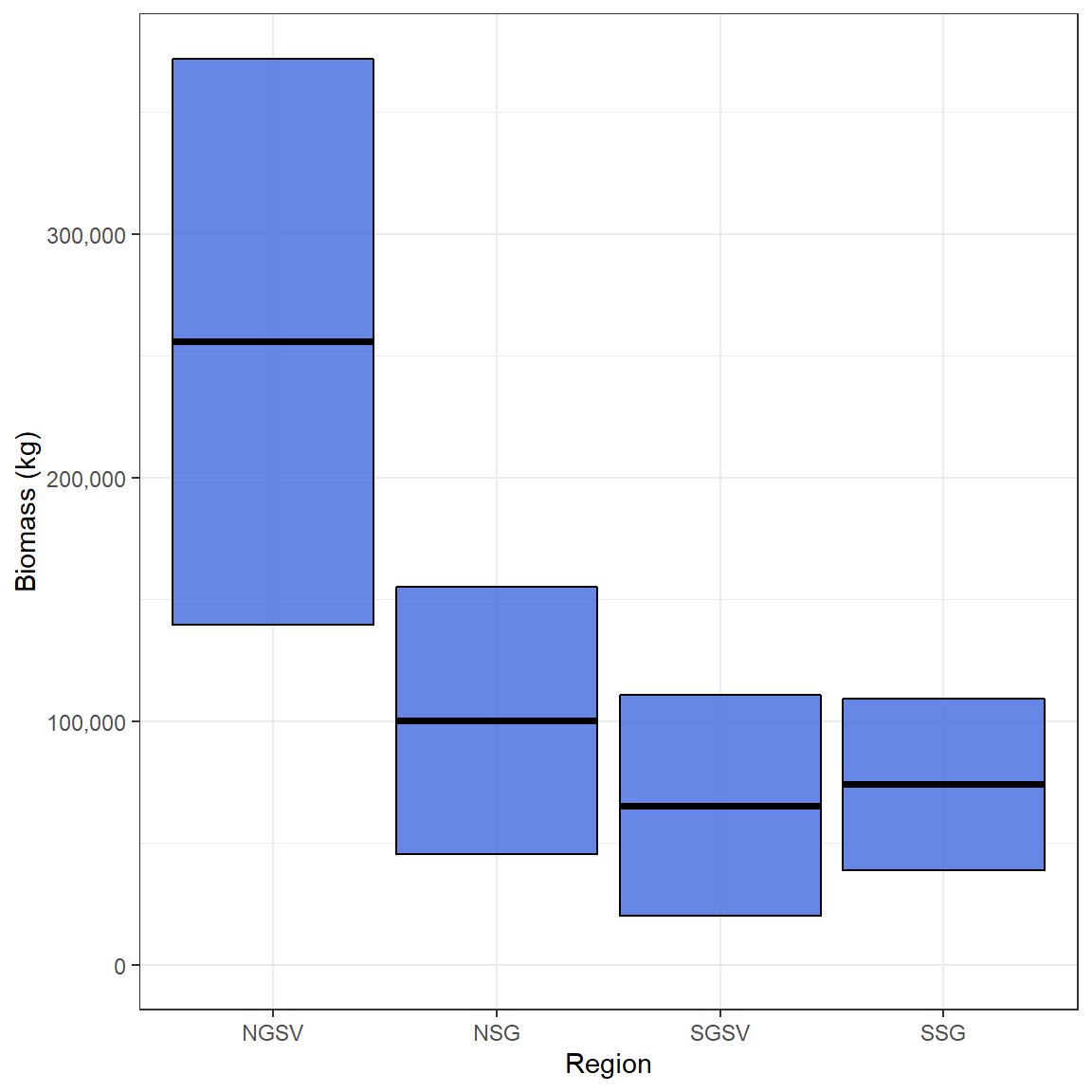
Plot total number of females

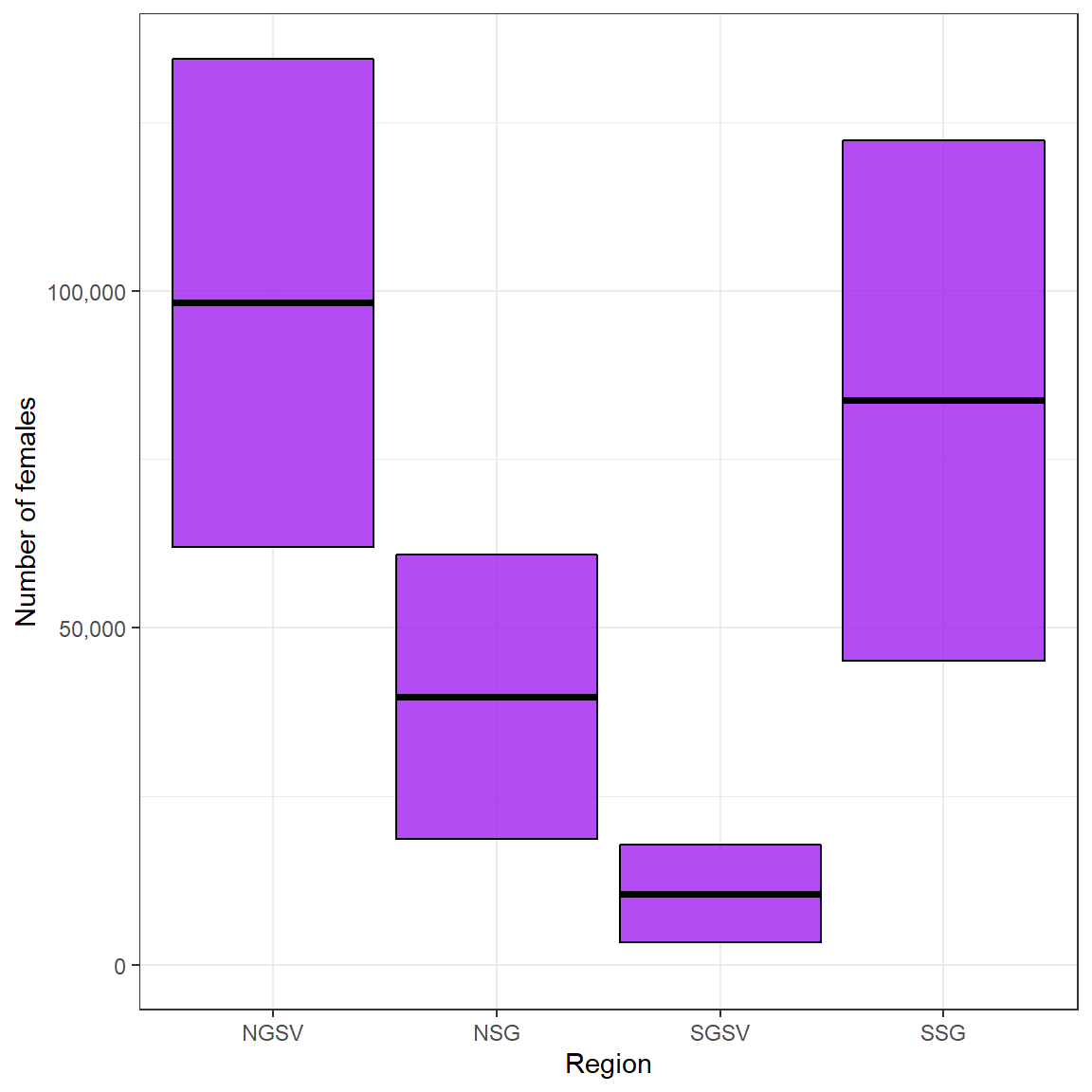
Testing assumptions for pre-specified egg mortality (Z)

As the \(P_{0}\) estimation methods in this package require a specified level of egg mortality (Z), it is sensible to test the sensitivities of the \(P_{0}\) estimates, as well as the DEPMWt results to different Z values. Testing different values of Z can be done by passing a vector of values to the z argument of Estimate_P0():

This will return a different \(P_{0}\) estimate for each value of Z for each Time/Region grouping:

For South Australian Snapper, the resulting \(P_{0}\) estimates are very similar.

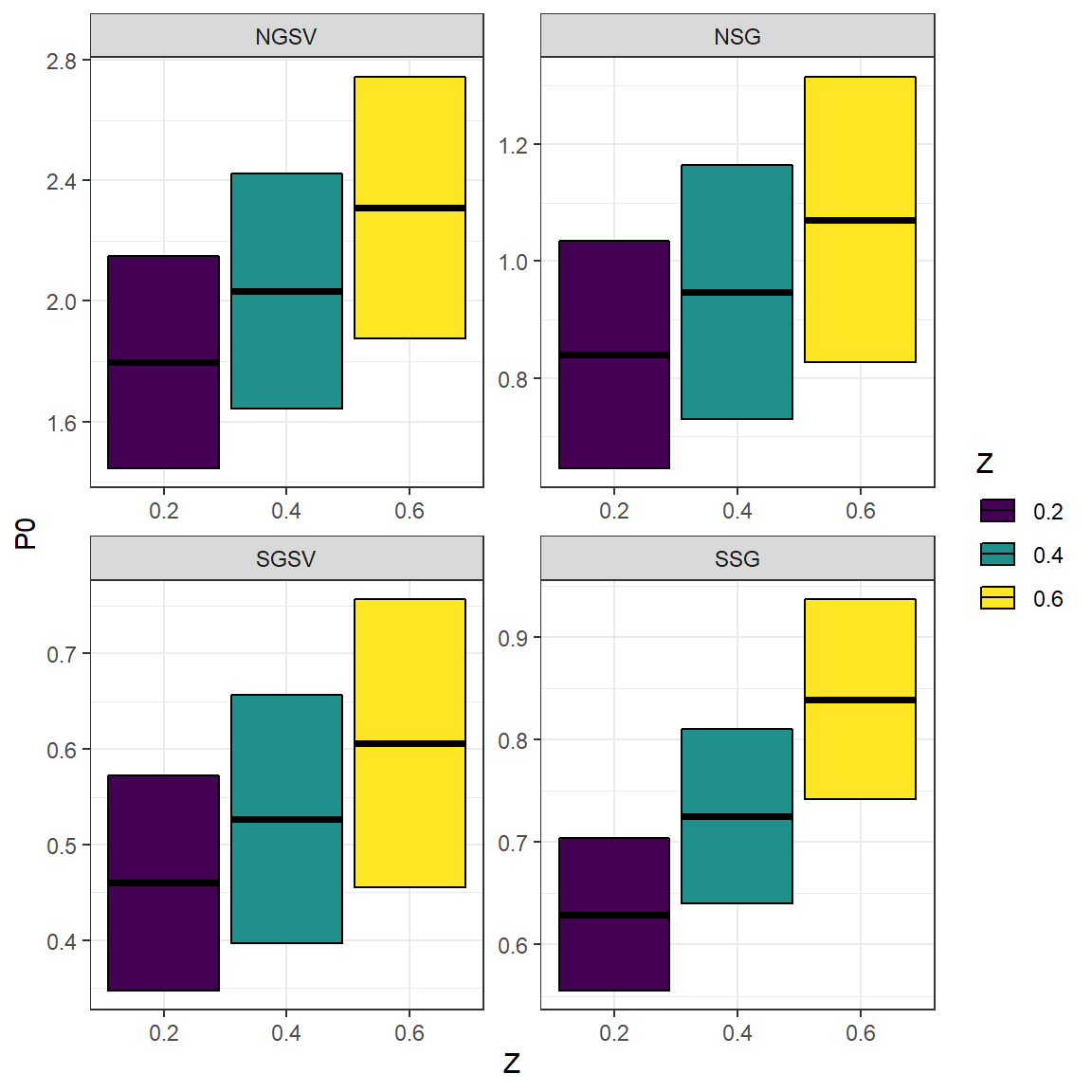
An object from Estimate_P0() with multiple Zs can be included in the biomass estimation procedure in the same manner as before. When multiple Zs are provided to combine_estimates() and combine_variances() they are treated as groupings and all other parameters will be aligned with them. When creating an object for spawning area A, care must be taken to only have unique Time/Region groupings. Using an object from Estimate_P0() with multiple Zs can erroneously add duplicates if you’re not careful. This will cause error messages.

A new object with Z as a grouping will now be produced which can be passed to the biomass estimation function.

These results can then be examined to determine how biomass is influenced by the specification of Z.

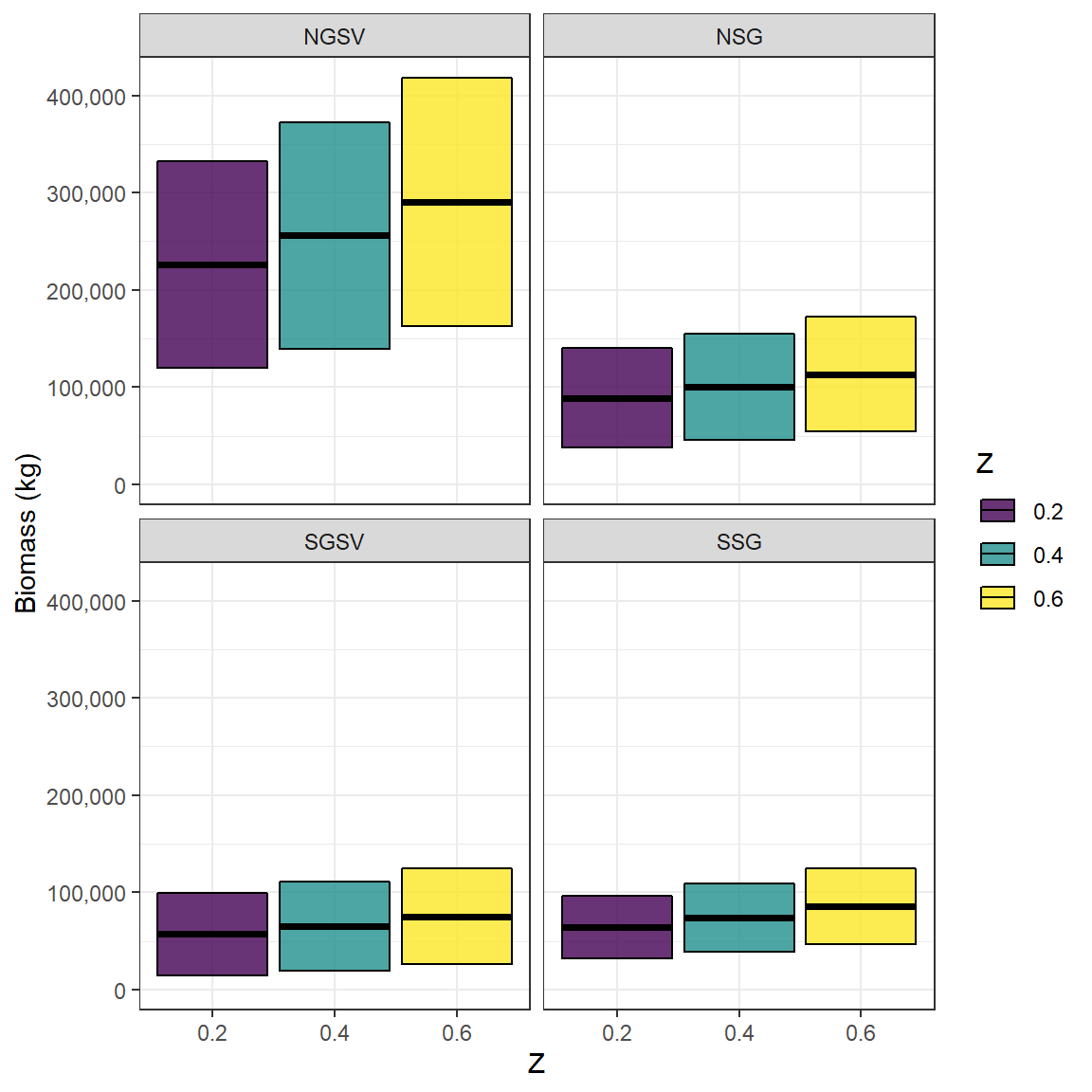
References

McGarvey, R., Steer, M. A., Smart, J. J., Matthews, D. J. and Matthews, J. M.(in review). Generalizing the Parker model equation of DEPM: incorporating size dependence of population numbers and batch fecundity

McGarvey, R., Steer, M.A., Matthews, J.M., Ward, T.M. (2018). A stage-based estimator of daily egg production. ICES J. Mar. Sci. 75(5), 1638-1646.